今天我们讲解第二种排序算法——选择排序。
问题
使用选择排序算法对列表中随机生成的10个数据进行从小到大排序,即最小的数字在最上面,最大的数字在最下面。
分析
选择排序也是一种简单直观的排序算法。它的步骤是: – 首先在未排序序列中找到最小(或最大)元素,存放到排序序列的起始位置。 – 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。 – 重复第二步,直到所有元素均排序完毕。
我们仍然用同学们排队的方式来演示这个过程。
上一次排队把老师累坏了,他决定换个方法,并且找了一只鸭子当助手,和他一起站在队首:

老师告诉鸭子:你去从前到后走一遍,把身高最低同学的位置告诉我。
鸭子说:可是我怎么知道谁身高最低啊?记不住啊!
老师说,你可以这样,现在站在排首的不是欢欢吗?我们先把最低同学的位置设置成他的,当然啦,这有点不符合实际情况,不过只要你向前走一个位置,发现这个位置的同学(可可)身高比欢欢低,就把最低身高位置设置成可可的位置;然后继续向前走,发现乐乐比欢欢还低,那再把最低身高的位置修改成乐乐的位置……这样只要你把一轮走完了,你就知道哪个位置的同学身高最低了。
“好的,明白了!” 鸭子说。按照老师教的方法,他从队首走到队尾,最终确定,第四个位置的同学格格的身高是最低的。于是指着格格说——老师,最低的位置是第四个!

“做得好!”老师夸奖了鸭子一句:“第四位同学,你过来,和排在前面的欢欢换一下位置”。于是格格和欢欢换了位置。这样第一个位置(也就是身高最低的同学确定了),格格就属于排好队的同学了。老师就向前走了一步到第二位,并要求鸭子重复上一轮操作,在剩下四个没排好的位置中找身高最低的。鸭子很快找到了第三位的乐乐:

“效率很高嘛!”,老师高兴地让第二位的可可和第三位的乐乐(也就是未排队同学中最低的)换了位置。然后老师和鸭子一起站到了第三位。

“老师,我看了一遍,好像剩下三位同学中可可就是最低的了呀,还让她和谁换呢?” 鸭子挠了挠头说。
“最低的正好是她自己,那就不交换了呗!”老师说,“下一个!”
于是,现在格格,可可、乐乐都进入了已经排好位置的序列,老师走到了第四位同学,也就是欢欢的位置,鸭子看了一遍说:第五位还是低一些。

“换!”老师一声令下,这一轮最小的位置和老师站的位置的同学换了位置。老师和鸭子都站到了第五位同学身边。

“老师,一共五位同学,后面没人了呀”鸭子大惊小怪地说。 “没人了,就代表全部排序完成了啊”。

于是 ,最后一个位置的同学也确定了,当然是大个子欢欢。
不知道你发现了没有,老师让鸭子每走一轮,都会找出“剩下”(也就是没排好队的同学)同学中身高最低的,然后和这一轮他站的位置互换。每找一轮,完成一次交换,他就向前走一个位置。等走到最后一个位置,排队就完成了。
编程
下面,我们把上述过程翻译成下面的自制积木:
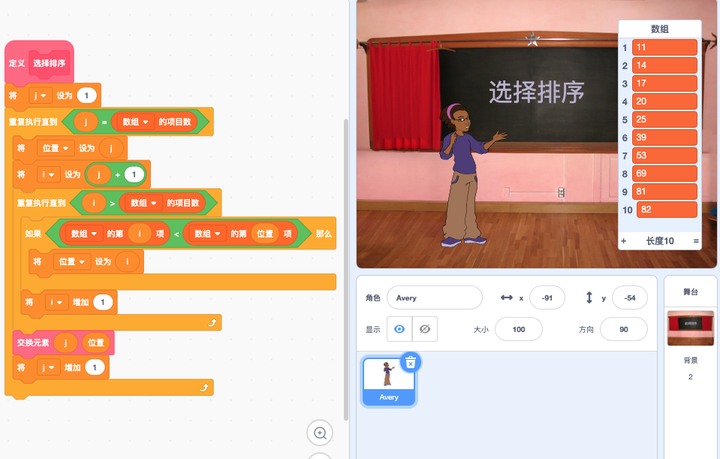
这里,$ j $ 变量代表老师的位置,开始排序的时候,他开始站在第一位,每排一轮向前走一步,直到走到数组项目数,也就是有几个人就走到第几个位置。在每一轮,鸭子会从老师位置的下一个出发向前走,我们用 $i $设置为 $ j+1$ 来表示,重复执行直至鸭子已经走到最后一个位置的后面(也就是 $ i > 数组项目数$ 的时候),这一轮就找完了。找完之后,用我们上一节做好的交换元素积木,把老师位置的同学与这一轮找出最低的同学交换就可以。
通过这个简单的两层循环,我们就实现了选择排序。
总结
选拔排序总共比较多少次?
- 第一轮:4次;
- 第二轮:3次;
- 第三轮:2次;
- 第四轮:1次;
- 第五轮:不比较了。
所以和冒泡排序一样,还是10次。如果要排序的序列数字很多,速度也会慢下来。我们容后再说。
