预备知识
从这一节课开始,我们要开始画一些“分形”图形。什么是分形呢?看下面这张图片:

这不是西兰花吗?它和分形有什么关系呢?
仔细观察,你会发现这棵西兰花是由许多个小一些的块组成的,每一块好像就是一朵缩小了的西兰花!就好像西兰花是由比自己小一号的克隆体组成的,而这些克隆体又是由比它们自己更小一号的克隆体组成,再小一号的克隆体由再再小一号的克隆体组成……如果你用放大镜看,最微小的西兰花组成部分和整棵西兰花好像是一样的!这种“整体就是局部、局部就是整体”的“自相似性”就是分形了。
自然界到处存在着分形,比如海岸线的形状、树的形状,包括我们的大脑和肺都是分形体。它就好像是大自然创造万物时的密码,让你不得不惊叹,原来那些看上去复杂的东西,都是由无数个简单的“克隆体”组合而成的!
分形在科学上有许多应用,我们现在先学会一些简单的分形画法就可以了,比如今天我们要画的是谢尔宾斯基分形。
谢尔宾斯基是波兰的一名数学家,他于1915年提出了谢尔宾斯基三角形,这就是一种“自相似”的图形,构造方法如下:
1、取一个实心的三角形。(多数使用等边三角形) 2、沿三边中点的连线,将它分成四个小三角形。 3、去掉中间的那一个小三角形。 4、对其余三个小三角形重复第一步。
这里“重复第一步”非常关键,正是这种重复才让这种图形的局部和整体是相似的。

如果取一个正方形或其他形状开始,用类似的方法构作,形状也会和谢尔宾斯基三角形相近。这种图形被称为“谢尔宾斯基地毯”。

今天我们就要画这两种分形图。
问题
使用Scratch画笔绘制谢尔宾斯基三角形和谢尔宾斯基地毯。
分析
要实现谢尔宾斯基三角形,我们无法去像现实中去从一个三角形中间“挖”去一个,但我们在画三角形每条边的时候,都画以它的一半边长先画个小的等边三角形,三条边总共画出三个,加上原来的大三角形,就构成一一个四等分三角形。
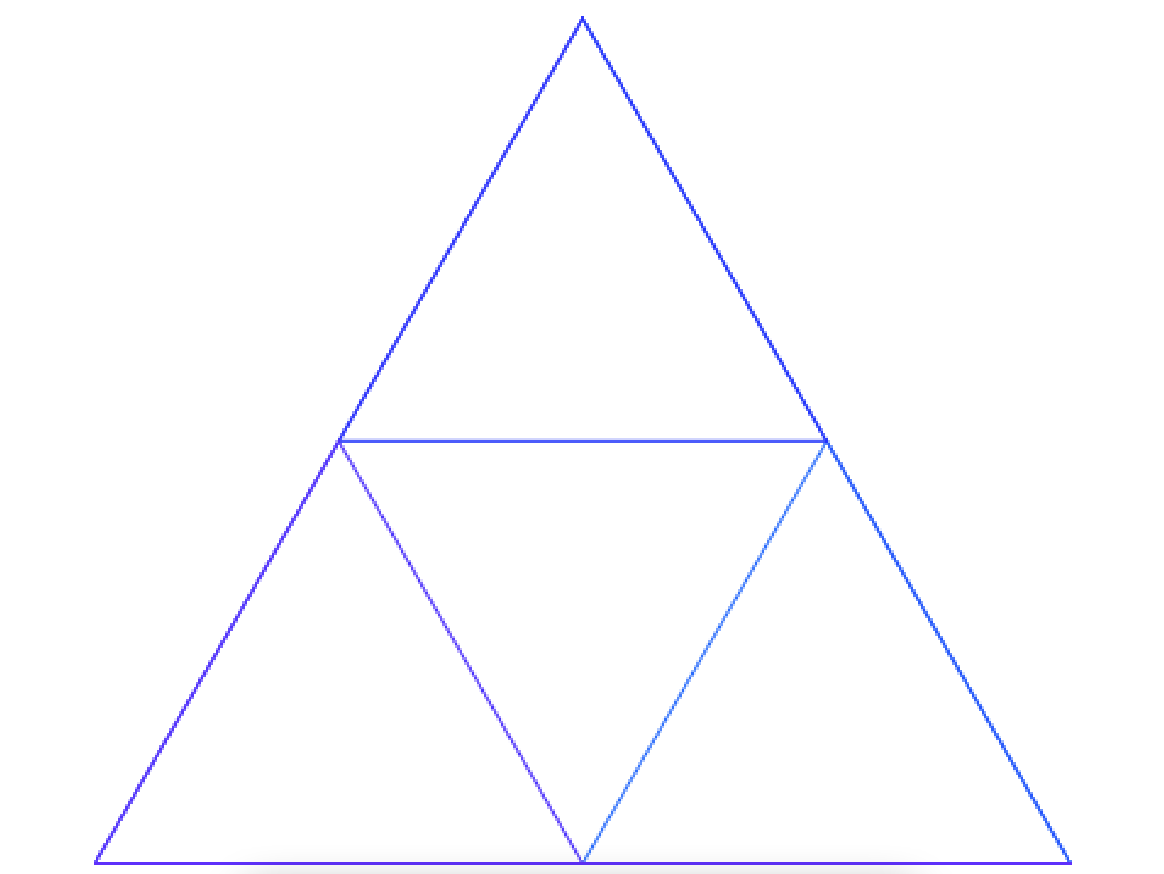
当然,在画小一半的三角形时,我们对它还可以重复这个过程。
以上过程让你你想到了什么?是的,自己调用自己的,这不是递归吗?我们正是要借助递归的特性来实现“分形”。
编程
一、根据分析,我们先来画一个等边三角形,这个过于简单,我就不解释什么了……

二、现在,你如果调用这个积木,会以你指定的边长画一个三角形。那么如果我在左转之前,先以一半的边长调用一下自己呢——

三、如果你现在调用这块自制积木,你的画笔角色将毫无响应,但是程序明明还在执行?这时候,赶紧停止程序。这是因为你让积木不断调用自己,它无休止地调用自己的二分之一的二分之一的二分之一……的边长画三角形,这是一个死循环,因为数字总能分到更小,你的计算机资源耗尽也算不完。因此,我们必须给这个程序加上限制,如果边长小于一定程度,比如20,就不再执行了——

这时运行程序,你的画笔开始上下翻飞,很快画出了你想要的结果——
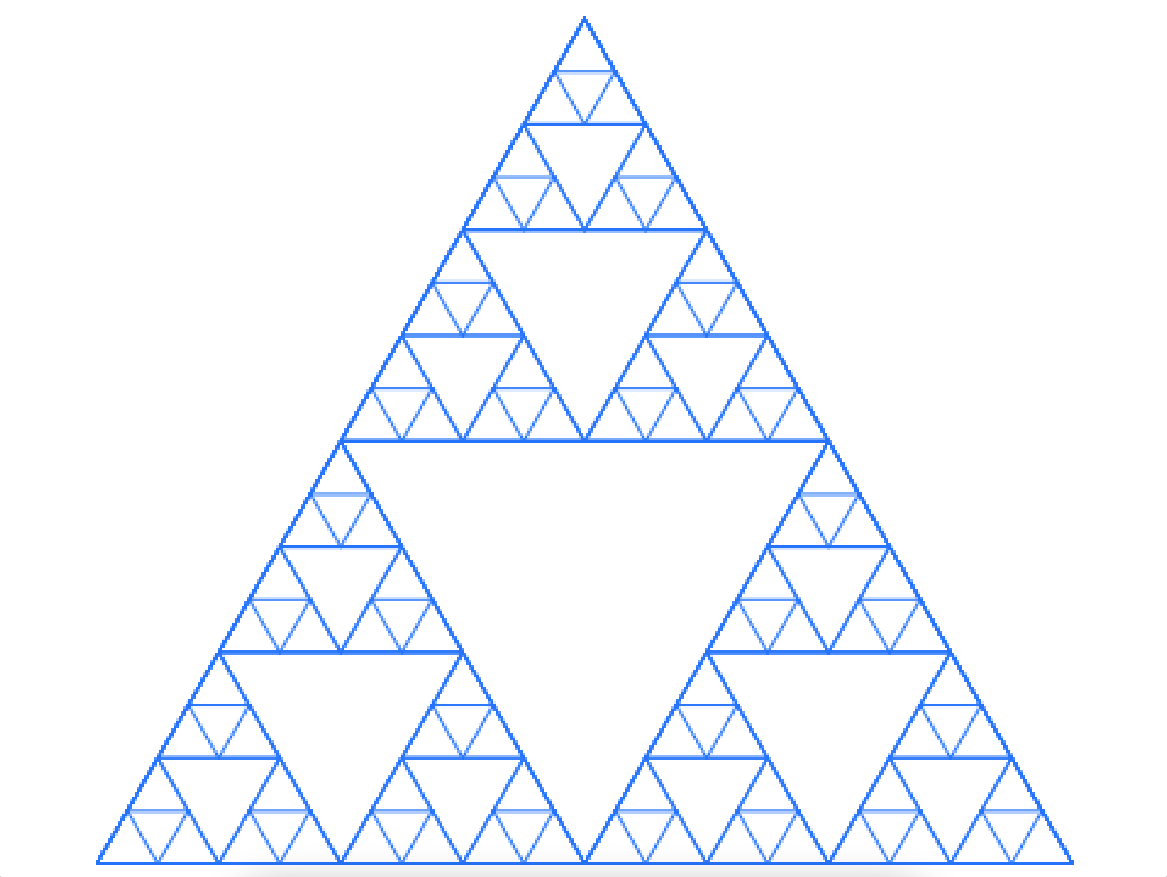
四、加上必要的初始化代码,在画三角形时加上修改画笔颜色的指令,你可以得到这样的结果(通过调整“等边三角形”自制积木中限制执行的边长,你可以画出更密集的三角形,当然速度也更慢):
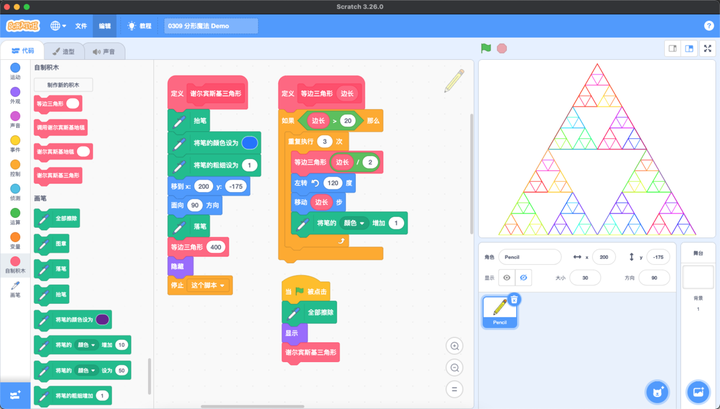
五、到这里我们画谢尔宾斯基三角形任务基本已经完成了,让我们再画一个以正方形为基础的谢尔宾斯基地毯 :
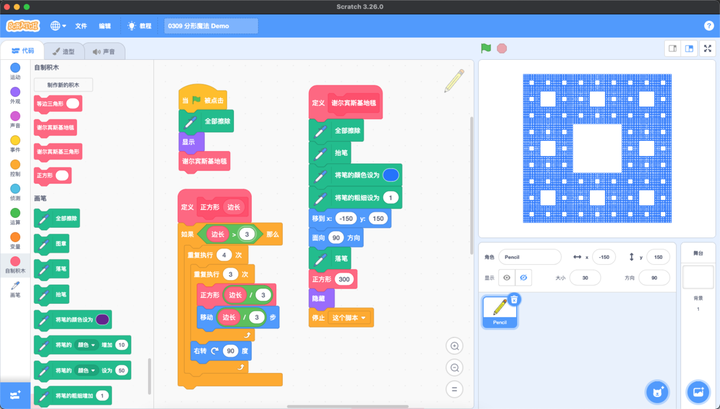
正方形画起来就慢多了,可以通过将自制积木设置为“运行时不刷新屏幕”来大幅度提升绘图速度。
六、演示一下画谢尔宾斯基三角形的过程:
总结
只需要给绘制等边三角形这样简单的自制积木加上递归调用,就能画出这么漂亮的图案,这就是分形的奇妙之处。当然,递归虽好,可不要忘记加限制条件哦!
