预备知识
一般从小学三年级开始,我们的数学课就开始学分数了。分数的意义是这样的:把单位“ 1” 平均分成若干份,表示这样的一份或者几份的数,叫做分数。在分数里,表示把单位“ 1” 平均分成多少份的数,叫做分数的分母;表示取了多少份的数,叫做分数的分子;其中的一份,叫做分数单位。
举例来说,把一个苹果切成四份,你吃掉了其中的两份,那就是四分之二,这就是一个分数。分数可以约分,比如可以把四分之二约分,变为二分之一。
关于分数还有以下概念:
- 分子、分母是互质数的分数,叫做最简分数;
- 把一个分数化成同它相等但分子、分母都比较小的分数,叫做约分;约分的方法是用分子和分母的公约数(1除外)去除分子、分母;通常要除到得出最简分数为止;
- 把异分母分数分别化成和原来分数相等的同分母分数,叫做通分;通分的方法是先求出原来几个分母的最小公倍数,然后把各分数化成用这个最小公倍数作分母的分数。
有了这些预备知识,让我们来看今天的问题。
问题
使用Scratch编写程序,实现两个分数的四则运算。
分析
用Scratch做数字的四则运算我们都很熟悉,因为Scratch已经提供了加减乘除的运算指令,只要用这几种运算符把两个数连起来,可以直接得到结果。不过我们今天要解决的是分数的四则运算,所以就必须按分数的规则来。我们可以回顾一下分数的运算规则(我们把两个数字称为分数1、分数2):
- 两个分数相加,如果是同分母,则结果的分母不变,结果的分子等于分数1的分子+分数2的分子;如果是异分母,先进行通分再将分子相加;比如:1/4 + 1/5 = 5/20 + 4/20 = 9/20。
- 两个分数相减,和加法类似。如:1/4 – 1/5 = 5/20 – 4/20 = 1/20。
- 两个分数相乘,只需要将分子分母分别相乘得到结果的分子和分母,再把得到的结果进行约分;例如:3/4 × 2/5 = 6/20,约分得到 3/10。
- 两个分数相除,需要把分数2先变成倒数再乘分数1,即把分数2的分子分母“倒”过来再和分数1相乘。例如:1/2 ÷ 1/4 = 1/2 × 4/1 = 4/2 = 2,原来分数2是1/4,变成了倒数4/1再和分数1相乘。
有了这些规则,要实现分数四则运算就容易多了,但还存在一个问题没有解决,怎么对计算的结果进行约分呢?约分就是分子分母同时除以它们的最大公约数,这就要用到“欧几里得算法”了。这个算法的计算步骤如下:
对于两个自然数a和b(规定a>b,即a是两个数中较大的一个),先用a除以b,得到余数c; 若余数 c 不等于0,就将b和c构成新的一对数(即将a设定为b,b设定为c),继续前面的除法,直至余数c为零。这里的b就是原来两个自然数的最大公约数。
这种算法需要反复进行除法运算,所以被形象地称为“辗转相除法”,又因为它是距今2300多年前的古希腊数学家欧几里得发明的(出自他的著作《几何原本》),又被称为欧几里得算法。
我们用欧几里得算法求到了结果分子和分母的最大公约数,约分就可以得到最终结果。
编程
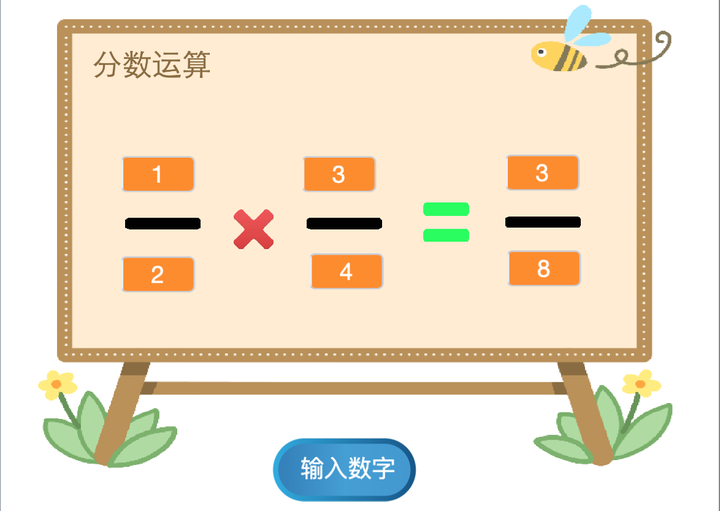
新建一个Scratch程序,建立分子1、分母1、分子2、分母2四个变量用于保存分数1和分数2的分子分母,把它们以大字形式显示在舞台上,然后我们把分数线(黑色的横线)、运算符(具有加减乘除四个造型的角色)以及等于号和这些变量的位置安排好,如图所示:
为了方便,我们先来定义一个自制积木,这个自制积木通过欧几里得算法来计算两个数字的最大公约数:
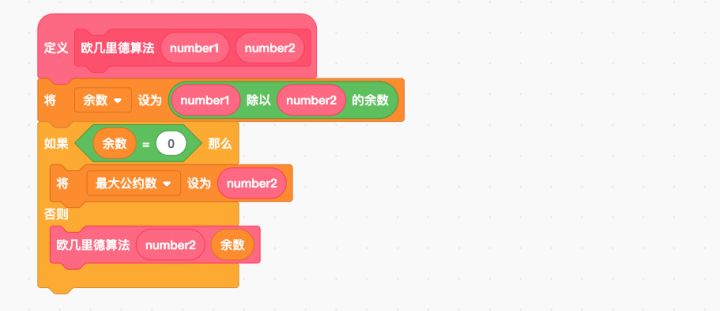
正如我们前面在分析环节描述的,它是通过辗转相除的方式计算最大公数数的,不过这里我们运用了一个技巧,就是当余数不为0时,这个积木又调用了一次自己(这种自己调用自己的做法被称为递归),把当前的number2和得到的余数又传递给自己,你可以把这里调用自己理解为生成了自制积木的一个克隆体,每调用一次自己,都生成了“欧几里得算法”这个自制积木的克隆体,并把参数传给他。当积木中的条件“余数为0”满足时,就不再调用自己了,把“最大公约数” 变量设置为number2,返回到调用自己的上一个克隆体并把当前克隆体删除,一直回到最初的自制积木本身,这个调用才结束。
有了这个自制积木,我们就很方便地实现分数四则运算了,首先你要把分子1、分母1、分子2、分母2这四个变量通过“询问”的方式让用户输入值,从而得到分数1和分数2,然后利用这四个变量进行加减乘除运算,关键代码是:
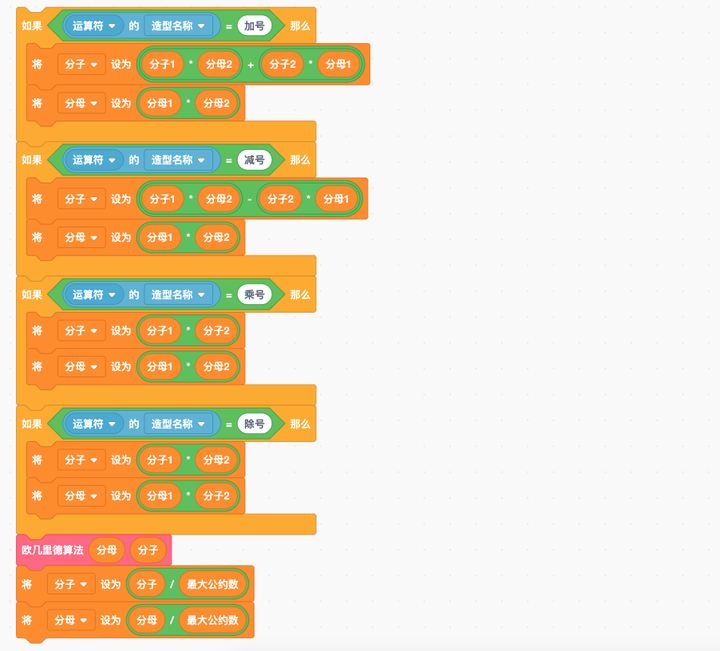
相信你可以看懂这段程序,如果不懂,你需要向上翻页,查看“分析”环节我们讨论的分数四则运算的计算规则。
有了这段核心代码,你可以在用户点击“运算符”角色时,切换运算符的造型,比如点一下从加号变成减号,再点一下变乘号、再点一下变除号,再点的时候又回到加号。一旦运算符变化了,意味着我们需要重新计算结果,这时只需要重新调用一下上面这段关键代码就行了。
程序最终的运行效果是这样的:
总结
乍一看分数四则运算,有点无从下手,但我们通过研究分数的四则运算法则,实际上把它转换成了四个变量的计算,这就回到了我们熟悉的领域,可以用Scratch提供的积木轻松实现了。这种把未知领域的问题转换成已知领域的问题的能力,不是一朝一夕可以练成的,需要我们不断地在编程中积累经验。
另外,我们在实现欧几里得算法时使用了递归的调用方式(积木自己调用自己),这是一种很强大的编程方法,以后我们会多次用到,但也要注意不能写错指令,否则很可能会把你的 Scratch 搞崩溃,原因呢,我们以后再说。
