二分查找是一种算法, 其输入是一个有序的元索列表 (必须是有序的),如果查找的元素包含在列表中,二分查找返回其位置,否则返回“没有该数据。比如,有一个1~100的数字,我随机地选择其中一个数字(假设为60),你需要以最少的次数猜到我所选择的数字,每次猜测后,我会告诉你大了、小了或对了。
假设你第一次从1开始猜,小了;第二次:2小了;第三次: 3小了;第五十九次: 59小了;第六十次: 60对了。
这是顺序查找。每次猜测只能排除一个数字,如果我想的数字是100,那么可能需要从1猜到100了。
那么有没有更好的查找方式呢?答案当然是有的。二分查找就可以!
如果我选的数字是60。
第一次:你从50 (1-00的一半)开始猜,那么我告诉你小了,就排除了接近一半的数字,因为你至少知道1-50都小了。
第二次:你猜75 (50-100的一半),那么我告诉你大了,这样剩下的数字又少了一半!或许你已经想到了,我们每次猜测都是选择了中间的那个数字,从而使得每次都将余下的数字排除了一半。
第三次:接下来,很明显应该猜测63 (50-75的一半), 大了。
第四次:然后你猜56 (50-63的一半),小了。
第五次:然后你猜59 (56-63的一半)小了。
第六次:猜测61 (59-63的一半),大了。
第七次,你就能很明确地告诉我,答案是60 (59-61的一半) !
这样的查找方式,很明显比第一种要高效很多。第一种需要猜测60次才能猜出正确答案,而使用第二种方式,只需要七次就能猜出正确答案。
或许看到这里你已经明白了,这就是分查找的方法。为什么分查找要求有序(升序或者降序均可),从这里也可以看出来。
用scratch实现二分查找数字案例:
从(10.20,30,40,50,60,70,80,90,100)有序序列中查找80的位置。
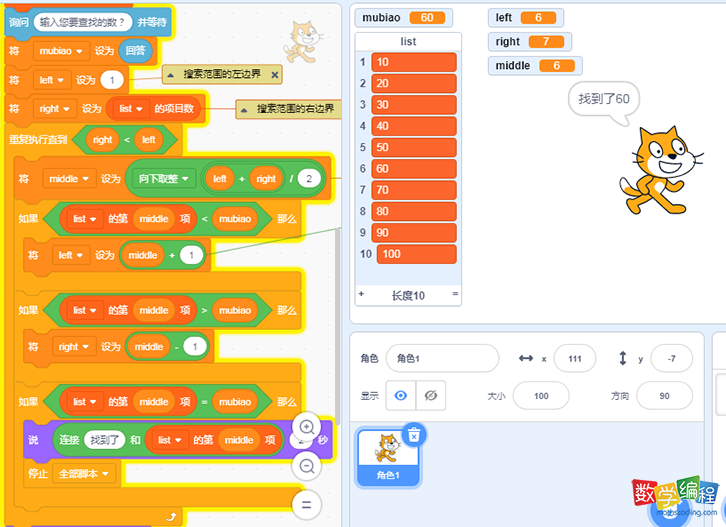
此实现过程的实施是通过变量left 和right控制一个循环来查找元素(其中let和right是正在查找的有序序列的左边界值和右边界值)。
用scratch实现二分查找数字
首先,将left和right分别设置为1和10。可下取整。在循环每次迭代过程中,将middle设置为left和right之间区域的中间值;
如left=1, right=10 时,middle 等于同下政型➊+❾/❷,也就是5。
如果处于midle的元素比目标值小,将左索引值移动到midle后的一个元素的位置上。
也就是letmiddle+1, right不变, 即下一组要搜索的区域是当前
数据集的右半区。
如果处于middle的元素比目标元素大,将右索引|值移动到middle前一个元素的位置上。
也就是right-=middle-1, left不变, 即下组要搜索的区 域是当前数据集的左半区。
随着搜索地不断进行,left 从左向右移,right 从右向左移。一旦在 middle处找到目标,查找将停止。如果没有找到目标,right 将小于left。
scratch二分查找算法实现步骤:
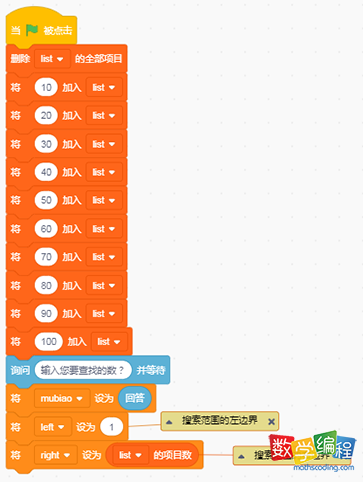
step1、建立一个“list”列表数据,并添加元素;
step2、建立一个变量“mubiao”代表查找的目标数字;建立一个left变量,代表要搜索范围左边界,初始值等于1;建立一个
right变量,代表要搜索范围右边界,初始值等于10 (此处只有10个元素);建立一个 middle变量,代表要搜索范围中央位置:如left=1, right=10 时,middle 等于向下取整➊+10/❷,也就是5。
初始变量
step3、随着搜索的不断进行,left从左向右移,right从右向左移。一旦在middle处找到目标,查找将停止;如果没有找到目标,right将小于left。

二分查找目标数字
scratch算法相关的重要知识点:
scratch选择排序算法
scratch冒泡排序算法
scratch少儿数学编程算法题:根据天数求苹果数量
