目录
- 1. 向量 & 矩阵
- 1.1. 问: np.ndarray 与 np.matrix
- 1.2. 向量空间
- 2. 算术运算
- 2.1. 为什么线性代数定义的乘积运算不按照加法的规则(按位相乘)进行?
- 2.2. 数组广播(broadcasting)
- 3. 矩阵乘积
- 3.1. 矩阵与向量的乘积
- 3.1.1. 除了坐标转换,矩阵乘积还有什么用?
- 3.1.2. 矩阵 * 矩阵
- 3.1.3. 一些特例
- 4. 点积乘法
- 5. 特殊矩阵
- 5.1. 转置矩阵
- 5.1.1. 共轭转置
- 6. 用矩阵表示各种关系
- 6.1. 高阶差分
- 6.2. 高阶微分
- 6.3. 消除常数项
- 7. 行列式
- 7.1. 行列式的性质
- 7.2. 行列式的计算
- 8. 逆矩阵 & 秩
- 8.1. 逆矩阵的性质
- 8.2. 对角矩阵的逆矩阵
- 8.3. 求解逆矩阵(numpy)
- 8.4. 秩
- 8.4.1. “秩”是图像经过矩阵变换之后的空间维度
- 8.4.2. “秩”是列空间的维度
- 8.4.3. 话说回来,为啥叫做“秩”
- 8.4.4. 求解秩(numpy)
- 8.5. 维数定理
- 9. 线性方程组
- 10. 特征值 & 特征向量
1. 向量 & 矩阵

向量(数组)的元素类型可以通过dtype属性获得。上面例子中的参数序列的元素都是整数,因此所创建的数组的元素类型也是整数,并且是32bit的长整型。可以通过dtype参数在创建时指定元素类型:
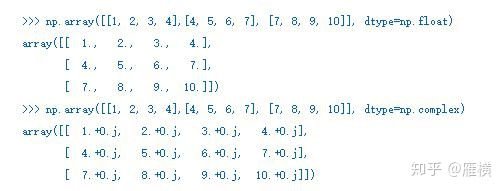
对,向量与 np.ndarray 不是同一个东西——向量就是一维数组。在几何意义上,向量表示的是多维空间中的有向线段,数组的每个数据代表了一个维度的参数。
而 ndarray 可以是多维数组,更像是Matrix。
1.1. 问: np.ndarray 与 np.matrix 的区别
1.2. 向量空间
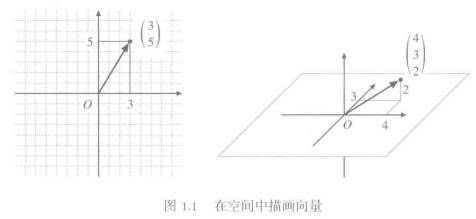
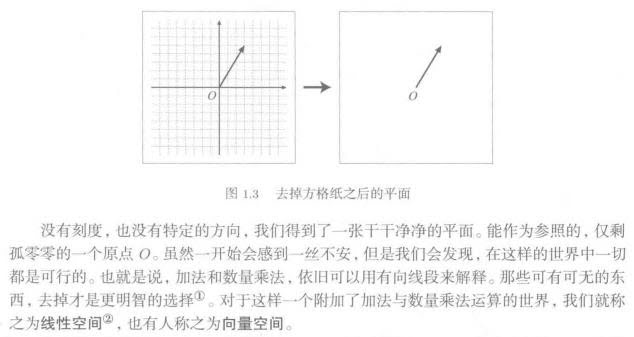
把上图中的刻度去掉,就是向量空间。
2. 算术运算


注意:numpy.ndarray的乘积运算,并不等同于线性代数中两个向量的乘积运算。
2.1. 为什么线性代数定义的乘积运算不按照加法的规则(按位相乘)进行?

线性代数的乘法运算(矩阵乘积),几何意义表示坐标系变换。
2.2. 数组广播(broadcasting)
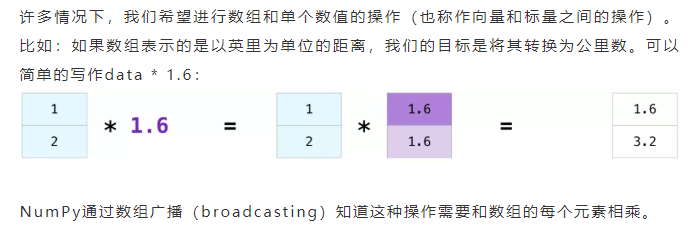
对于不同大小的矩阵,只有两个矩阵的维度同为1时(例如矩阵只有一列或一行),我们才能进行这些算术运算,在这种情况下,NumPy使用广播规则(broadcast)进行操作处理:

3. 矩阵乘积
3.1. 矩阵与向量的乘积
两种情形:

矩阵 * 列向量 = 新向量(列)
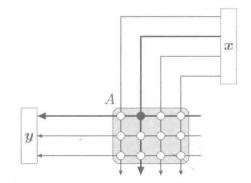
在这个过程中,向量代表的是一个有向线段,而矩阵则表示一个转换坐标系(或者称之为“线性的函数映射”),通过乘法运算后,向量被映射成了另一个坐标系中的样子。
所以,看懂了矩阵乘积,就能明白矩阵的本质——“矩阵就是映射”。
3.1.1. 除了坐标转换,矩阵乘积还有什么用?



3.1.2. 矩阵 * 矩阵
矩阵之间相乘,其本质就是映射的合成。

其实上述公式可以做如下转换:
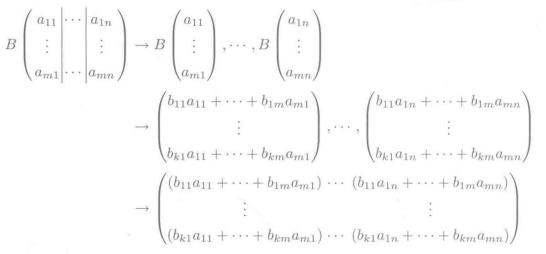
这是啥?其本质就是:
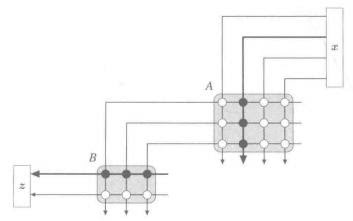

读懂这个本质,就能知道,矩阵乘法符合结合律:
C(BA) = (CB)A
但不符合交换律:

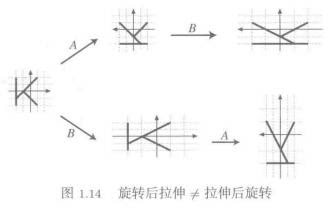
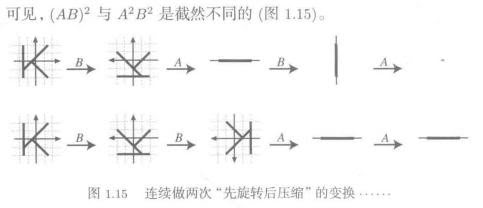
为什么矩阵乘法不符合交换律?
考虑A是一个旋转的坐标变换,而B则代表横向拉伸。那么先旋转后拉伸与先拉伸后旋转,结果当然不同。
3.1.3. 一些特例
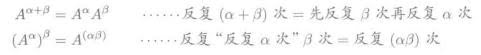
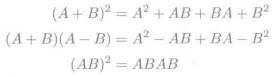
4. 点积乘法
5. 特殊矩阵
- 零矩阵
零矩阵表示的映射是所有点都映射到原点的映射。 - 单位矩阵
“什么都没变”的映射。
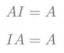
- 对角矩阵
对角矩阵表示的映射是“沿着坐标轴伸缩”,其中对角元素就是各轴伸缩的倍率。

- 分块矩阵
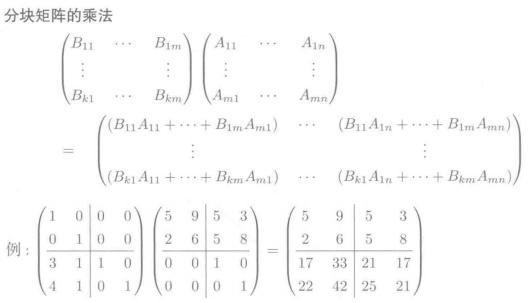
- 正交矩阵
- 对称矩阵
5.1. 转置矩阵

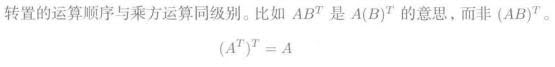

5.1.1. 共轭转置

6. 用矩阵表示各种关系
6.1. 高阶差分
6.2. 高阶微分
6.3. 消除常数项
7. 行列式
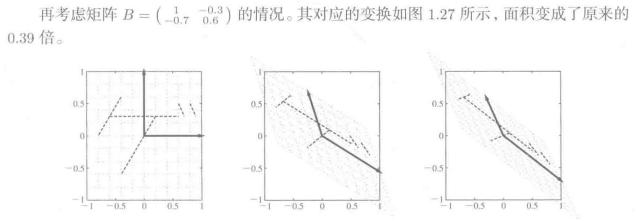

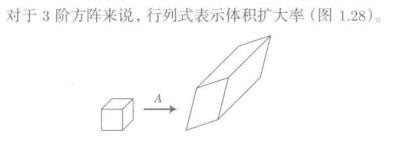
行列式求得的是一个数,几何意义为(面积、体积…)的扩大率。
行列式只针对方阵而言,非方阵矩阵不存在行列式。
7.1. 行列式的性质


常数乘法不变性
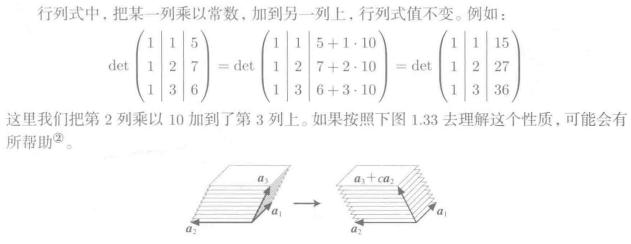
转置矩阵的行列式

多重线性
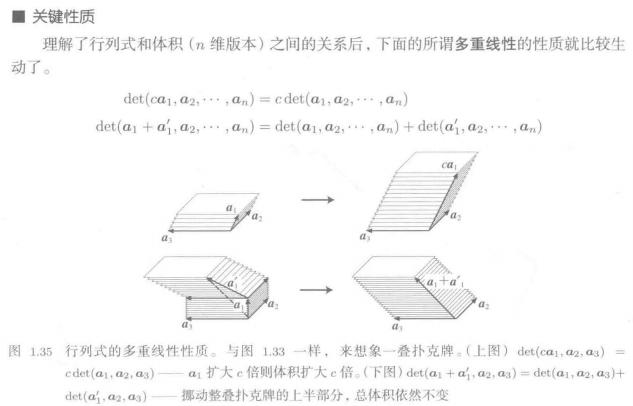

注意:多重性质都是针对1列定义的:

交替性
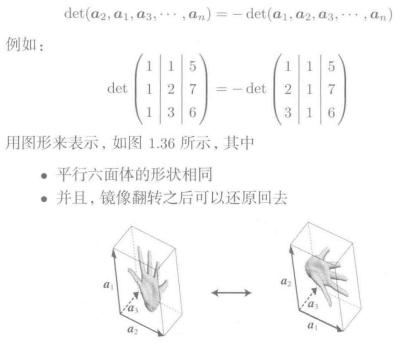
7.2. 行列式的计算
from numpy import linalg
n = linalg.det(A)8. 逆矩阵 & 秩
如果 y = Ax + b 为 顺问题 ,那么,通过 y 求得 x 的问题就是 逆问题 。
逆矩阵就是把矩阵A映射的向量还原回去的映射。简单的说,就是“逆映射”。

- 正则矩阵:存在逆矩阵的方阵(可逆矩阵,非奇异矩阵)
- 奇异矩阵:反之~
8.1. 逆矩阵的性质

![]()
8.2. 对角矩阵的逆矩阵

8.3. 求解逆矩阵(numpy)
from numpy import linalg
invA = linalg.inv(A)8.4. 秩
秩,体现的是不相关的维度数。
8.4.1. “秩”是图像经过矩阵变换之后的空间维度
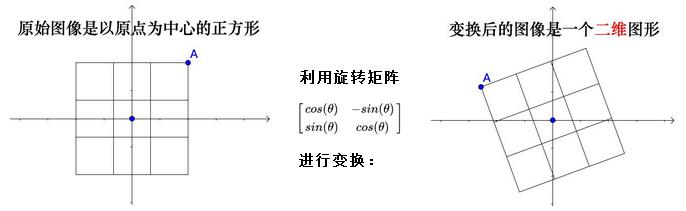
- 如果经过矩阵
A变换后的结果是一个平面,空间没有被压缩扁平化,那么该转换可逆,称为非奇异矩阵 - 非奇异矩阵的秩与列数相等,称之为满秩(Full Rank)矩阵
- 对于满秩矩阵来说, 变换后唯一落在原点的就是零向量本身
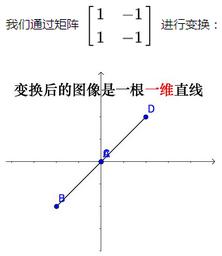
- 当变换的结果是一条直线,该矩阵是一维的,
rank(A) = 1,此时矩阵不可逆, 称为奇异矩阵 - 非满秩矩阵,会将空间压缩到更低的一维直线上,也就是由嫩绿色直线上一系列的向量在变换后成为零向量
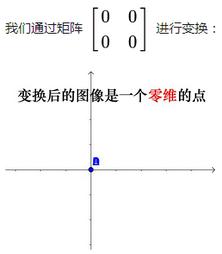
- 当变换的结果是压缩到原点,则该矩阵是零维的,称
rank(A) = 0
8.4.2. “秩”是列空间的维度
“秩”就是矩阵所代表空间的不相关的维度数量。而不相关的的维度才构成空间,所以,“秩”代表空间的维度。
8.4.3. 话说回来,为啥叫做“秩”
知乎: 非叫“秩”不可,有秩才有解
举个例子就很容易理解,大家排队买票。如果大家互相不认识,那就会一个排一个,非常有秩序。然而,如果突然来了一个与队伍前面的人认识的人,这个人又不自觉,非要插队。那后面的人肯定要有意见了,说你要是这样我前面还有认识的人呢,你插我也插,这样整个队伍就乱掉了,谁也买不成。
通过这个例子,可得以下结论:彼此不认识,那就不相关,就有秩序,问题就好解决;反之,彼此相关,就没有秩序,问题就不好解决。
所以,数学家们定义,矩阵中的最大的不相关的向量的个数,就叫秩,可以理解为有秩序的程度。
从社会学的角度在考虑一下,政府机关是讲人际关系的地方,可谓是关系错综复杂,通常都是近亲繁殖。显然,这些部门,用矩阵来说,就不满秩,秩非常小。可以想象这些地方的工作肯定是搞不好的,因为没有秩序。所以想找个好单位,满秩可以作为一项评价指标哦~
8.4.4. 求解秩(numpy)
from numpy import linalg
n = linalg.matrix_rank(A)8.5. 维数定理
- 向量空间的维数等于对应矩阵的秩
- 两个有限维子空间的和的维数定理:
dim(U1+U2) = dimU1 + dimU2 - dim(U1 ∩ U2) - 两个有限集合元素个数的容斥原理:
card(U1∪U2) = cardU1 + cardU2 - card(U1 ∩ U2)
